Measures of Central Tendency and Measures of Dispersion

What is central tendency?

By describing the central tendency of a set of data, statisticians attempt to summarize the entire set using only one number. The center or average (mean); middle value or halfway point (median); or typical or most common value (mode) all attempt to summarize the data. These summaries represent three different ways to report the central tendency. Why are there different ways to determine this summary? The reason relates to the levels of measurement that were introduced previously. Let's explore these three measures (also called descriptive statistics) within the context of an example and learn when each is appropriate to use.

Before introducing the mean, there is another term that you should know. A set of data is called a distribution. In the remainder of these notes, the term, distribution, will be used to describe a set of data or numbers that have been collected and that represent different quantified observations of phenomena.

The Mean (M or X)

You probably know this descriptive statistic better by its more common name, the average. Because there are many averages, statisticians like to be more precise with the terms they use. So, what you probably refer to as the average of a distribution, we will join statisticians in calling the mean, or arithmetic mean, to be very precise. There are other forms of means that you may see in research reports but which are infrequently used. Before explaining the routine to calculate this number, consider what it represents. One way to think of this number is the following. Suppose you had 10 test scores, and you had a brick for each score (all equally weighted). Then suppose you had a board that had the scale for the scores drawn on it. One end would represent 0% and the other would represent 100%. The board is balanced, without any scores on it yet, at 50%, which is halfway between the two ends. Now you place the 10 bricks on the scores that they represent, stacking them up if two scores are the same. When you finish placing the bricks, it is very likely that the board isn't balanced at 50% anymore. Instead you will have to adjust the board until it is balanced. The number on the test score scale that matches the balancing point is the mean score. Getting bricks and a board and balancing the arrangement of bricks isn't the most efficient way to calculate the mean. Let's look at the calculation steps instead.
  1. Add up all of the values (e.g., test scores)
  2. Divide the sum in Step 1 by the number of values (e.g., number of tests)
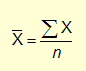
The mathematical formula looks like this: 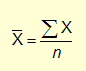X-bar equals summation of Xs divided by number of values

The first step of adding all the numbers happens quite frequently in statistical calculations; so statisticians have chosen to use the uppercase Greek letter sigma, ∑, to represent summation. Just remember the S in Sigma and the S in Summation to link the symbol with the process. Also n represents the number of values that we're adding. The symbols used for the mean include M and X, pronounced X-bar.

Now let's use the formula with a small distribution of test scores. Even though this example will only involve a few scores, the procedure for calculating the mean is the same no matter how many scores there are.

Scores:  7, 5, 8, 9, 7, 6, 9, 8, 7, 4

Step 1.    Add the values.    ∑X = 7 + 5 + 8 + 9 + 7 + 6 + 9 + 8 + 7 + 4 = 70
Step 2.    Divide by the number of values.    X = 70/10 = 7

If you have Excel, you can use it to calculate the mean. First, enter the numbers in a column - one number in each cell. Let's say that the numbers are in cells A1 through A10. Then, enter the following formula in cell A11 (or any other empty cell): = average(A1:A10)

That should be fairly straightforward. So, why isn't the mean sufficient for describing central tendency for all distributions? There are two reasons. The first reason is that the first step in the process, namely adding the values, doesn't always make sense. Think of a variable that represents ethnicity. Different ethnic classifications are arbitrarily assigned different numerical values. African American may be assigned a 1, while Asian is assigned a 3, and Caucasian is assigned a 5. Because these assignments are arbitrary, the actual values, as quantities, mean nothing. So adding them together would make no sense. Calculating a mean score for ethnicity would result in a meaningless number. Means make no sense for variables measured at a nominal level.

The second reason involves the mean's sensitivity to extreme values. What does this refer to? Recall the bricks and board example (or think of a teeter-totter). Placing a new brick near the middle (balancing point) has only a small effect on the balance, but if you placed a new brick at one of the far ends, it would have a great effect on the balance. This effect is larger when there is a small number of bricks. The brick on the far end is called an outlier. The presence of outliers makes the mean inaccurate as a measure of the center. An alternative measure of central tendency is needed in situations with outliers.

The Median (Mdn)

The second central tendency measure we'll study is the median. Think of the median as the middle point or halfway point of a distribution. Here is an example. Let's say that you had a group of nine middle-school students. As is often the case at this age, one of the students is unusually tall compared with the others in the group. Calculating the mean would be inappropriate because of the effect this one unusually tall student would have on the calculated mean. Instead, you decide to describe the "average" height as that of the halfway point. The first step is to line up all of the students according to their height - shortest to tallest. Then, because there are nine students, you go to the fifth student and measure her height. Her height is the median height for the group. Why? Because there are four students who are taller than she is and four students who are shorter than she is. So, the two steps for determining the median are to 1) sort the values and 2) pick the middle value. If you are following along closely, you should have a question - what if there is an even number of values. Suppose we have 10 students instead of 9 - how is the median determined in this case? There is just a slight twist - instead of picking the one middle value (because there isn't just one), you pick the middle two values. In our example of 10 students, the middle two are the fifth and sixth students. Then you average their heights by adding their heights and dividing by 2. Their average is the median for the group.
  1. Sort the values from smallest to largest
  2. If there is an odd number of values, choose the middle value. If there is an even number of values, choose the middle two and average them - add them and divide by 2.
Scores:  7, 5, 8, 9, 7, 6, 9, 8, 7, 4

Step 1.    Sort the values.    4, 5, 6, 7, 7, 7, 8, 8, 9, 9
Step 2.    Because there are 10 scores, pick the middle two scores, which are 7 and 7. Add them, 7 + 7 = 14, and then divide by 2, 14/2 = 7.

If you have Excel, you can use it to calculate the median. First, enter the numbers in a column - one number in each cell. Let's say that the numbers are in cells A1 through A10. Then, enter the following formula in cell A11 (or any other empty cell): = median(A1:A10)

The median is insensitive to extreme values. In the example, you could replace one of the 9s with 100 and the median would not change. Likewise, you could replace the 4 with a 0 and the median would not change either. This illustrates the insensitivity of the median to extreme values. There are situations when neither the mean nor the median is appropriate to use. Because the first step in determining the median requires that the values be sorted, the measurement level of the variable must be at the ordinal level or higher. Like the case with the mean, reporting a median score for a nominal variable is meaningless. 

The Mode

So you have a nominal variable, like ethnicity, and want consolidate the information and present a summary of this variable. Neither the mean nor the median is appropriate to use for nominal variables. Your only remaining option is to report the mode. The mode represents the most frequently occurring value. For the ethnicity variable, the mode represents the largest ethnic subgroup for a group of people. You might use the mode for other nominal variables, such as gender, eye color, or handedness. There might be occasions in which the mode helps you understand other types of variables. If you are arranging a classroom for groupwork, the mode for group size would tell you how many students to put at the most tables. If you are ordering graduation caps and gowns, the modes for cap size and gown size indicate the most common size to order. Someone ordering shoes for a store would order more shoes for the modal (adjective for mode) foot size. Someone arranging tables at a restaurant would set the tables for the modal dining party size. Let's see how the mode is derived.
  1. List the unique values that occur.
  2. Tally the number of occurrences for each value - the one with the largest tally is the mode.
Scores:  7, 5, 8, 9, 7, 6, 9, 8, 7, 4

Step 1.    List the unique values that occur.

Values
4
5
6
7
8
9

Step 2.    Tally the occurrences

Values Tally (frequency)
4 1
5 1
6 1
7 3
8 2
9 2

So, what is the mode? Is it 7 or 3? The mode is the most frequently occurring value, which is 7. The number of times that the modal value occurs is 3. So, in this example, the mode is 7. Notice that for this distribution the mean, median, and mode are all the same. This happens in certain situations but in most cases these three descriptive statistics will be different. Notice that in this distribution there is only one mode. Sometimes there are two modes or even more. In the context of education, you may have heard a group of students referred to as being bimodal, which would indicate that there are two distinct groups - perhaps good readers and struggling readers, for example. 

If you have Excel, you can use it to calculate the mode. First, enter the numbers in a column - one number in each cell. Let's say that the numbers are in cells A1 through A10. Then, enter the following formula in cell A11 (or any other empty cell): = mode(A1:A10)

Main Ideas about Central Tendency

What are the main ideas to remember about measures of central tendency?
Whenever something is summarized, numerically or otherwise, information is lost. Furthermore, when you choose a particular measure to represent a distribution, you are forced to make a compromise. Statisticians have introduced alternative measures of central tendency to reduce the limitations of the more traditional measures. For example, you may read about the trimean or trimmed means. The trimean involves a weighted average of the median with two other numbers that we'll meet in the next section, called the first and third quartiles. In calculating a trimmed mean, some percentage of the extreme scores are ignored and a traditional mean is calculated using the other scores. You may have seen trimmed means in action during judged sporting events, such as Olympic performances, where the highest and lowest marks are thrown out and the score is determined from the remaining judges' marks. 

The subject of the next section addresses the need to describe the spread of scores in addition to their central tendency. With these two descriptive statistics, more summary information can be provided.

What is dispersion?

Deriving one of the measures of central tendency provides some idea about the center of a distribution, but you might want to report how well the derived measure of central tendency represents the other values in the distribution. Stated another way, you might want to indicate how much the other values in the distribution are spread away from the center. They may be closely grouped around the center, or they may be quite widespread. Dispersion refers to the spread of the scores in a distribution. Other synonyms for dispersion include differences, spread, deviation, and variability. It is extremely important to realize that these measures of dispersion apply to ordinal-level variables or higher - dispersion, as it will be covered here, does not apply to nominal variables.

The Range

The first measure of dispersion that we'll consider is the range. The range represents the distance between the smallest value in the distribution and the largest value. For example, if the smallest is 3 and the largest is 9, then the range equals the difference between the two, 9-3 or 6. Notice that the range depends on two numbers only - the maximum value and the minimum value. None of the other values in the distribution affect the range. The other numbers could be grouped close to the mean or grouped near the extremes. As a result, the range by itself provides little information about the spread of the distribution. Here's how the range is calculated.
  1. Locate the maximum value (Max) and the minimum value (Min).
  2. Subtract the minimum value from the maximum value. Range = Max - Min.
Scores:  7, 5, 8, 9, 7, 6, 9, 8, 7, 4

Step 1.    Max = 9 and Min = 4
Step 2.    Range = 9 - 4 = 5

If you have Excel, you can use it to calculate the range. First, enter the numbers in a column - one number in each cell. Let's say that the numbers are in cells A1 through A10. Then, enter the following formula in cell A11 (or any other empty cell): = max(A1:A10) - min(A1:A10)

The Interquartile Range

There is another type of range that we will see later when we look at graphs of distributions. It is called the interquartile range and can be thought of as the range for the middle 50% of the values in the distribution. Think of a distribution being sorted and then divided into four groups - the first 25%, the second 25%, the third 25%, and the fourth 25% of the scores. The values that separate these four groups are called the quartiles. We already studied the second quartile (Q2), because it is the median or halfway point, or 50th percentile, of the distribution. Half of the values occur above the median and half below. Twenty-five percent of the values occur below the 25th percentile or Q1 or the first quartile, and 75% of the values occur below the 75th percentile or Q3 or the third quartile. The interquartile range is defined as the difference between Q3 and Q1. Because calculating the quartiles and the interquartile range requires more information about the distribution, it is viewed as a more stable measure of a distribution's spread. It also plays an important role in visually portraying a distribution using a boxplot, which we'll see later. One final note - because the interquartile range only requires the values to be sorted to find Q1 and Q3, it is an appropriate measure for ordinal-level variables or higher. We won't be calculating this statistic much, but you will see it used in the next section.

The Standard Deviation

For interval and ratio-level variables, where we are able to calculate the mean of a distribution, you might be thinking that it might be informative to derive some sort of average for how the values are spread out around the mean. For example, if the average spread is large, then the values are not grouped near the mean, and if the average spread is small, then the values are grouped close to the mean. Statisticians have derived just such a statistic; however, due to one of the properties of the mean, the simplest way to calculate the average spread always (yes, always) results in an average spread of 0. Consequently, the calculation of this average spread statistic, called the standard deviation, is more complicated. Understanding this calculation and what a standard deviation represents is extremely important for the rest of the material in the course and for correctly interpreting and using statistics in education in general. As you read through the steps, realize that Excel or SPSS performs the calculation for you, but you need to understand how these programs derive the statistic.

First, a bit of terminology. What is a deviation and what might make it standard? A deviation is the distance between a value in a distribution and the mean. Every value in the distribution has a deviation associated with it. Because the process of averaging deviations always results in a value of 0, there is no average deviation. Instead, statisticians use a process of squaring the deviations, averaging them, and then taking the square root of the result to generate a standard deviation. [Squaring is multiplying a number by itself - 3 squared is 3X3 or 9. Taking the square root is the opposite operation - the square root of 9 is 3. For numbers that are not perfect squares, like 4, 9, 16, 25, 36, 49, 64, 81, and 100 are - among infinitely many others, it is handy to have a spreadsheet program or a calculator.] Here are the steps and the formula for the standard deviation. Refer back to these steps to understand the example presented after the formula.

  1. Calculate the mean, X.
  2. Subtract each value from the mean - these are the deviations.
  3. Square the deviations.
  4. Sum the squared deviations.
  5. Divide the sum of squared deviations by n-1 - this is called the variance.
  6. Calculate the square root of the variance - this is the standard deviation.
The mathematical formula looks like this: standard deviation equals square root of summation of squared deviations divided by n-1

If you have Excel, you can use it to calculate the standard deviation. First, enter the numbers in a column - one number in each cell. Let's say that the numbers are in cells A1 through A10. Then, enter the following formula in cell A11 (or any other empty cell): = stdev(A1:A10)

Scores:  7, 5, 8, 9, 7, 6, 9, 8, 7, 4

Step 1.    The mean that we calculated earlier is X = 7.
Step 2.    The deviations are shown in the second column below.
Step 3.    The squared deviations are shown in the third column below.
Step 4.    Summing the squared deviations gives 24, as shown in the third to last cell of the third column.
Step 5.    Dividing 24 by n-1 (10-1=9) gives 2.67, as shown in the second to last cell of the third column.
Step 6.    Calculating the square root of 2.67 gives 1.63, as shown in the last cell of the third column.

X X-X (X-X)2
7 7-7=0 0X0=0
5 5-7=-2 -2X-2=4
8 8-7=1 1X1=1
9 9-7=2 2X2=4
7 7-7=0 0X0=0
6 6-7=-1 -1X-1=1
9 9-7=2 2X2=4
8 8-7=1 1X1=1
7 7-7=0 0X0=0
4 4-7=-3 -3X-3=9

sum of squared deviations 24

sum divided by n-1 (9) 2.67

square root (standard deviation) 1.63

Just to reiterate, no one calculates the standard deviation by hand following the steps listed here; however, understanding that the standard deviation is a measure of the amount of variation (or spread) in a distribution is very important. For example, if you have two standard deviations for similar sets of data and one is quite a bit larger than the other, the means that describe the centers of the two distributions are not equally accurate. The mean with the smaller deviation is a better summary of the distribution than the mean with the larger standard deviation. Think of the standard deviation as a quality-control measure for the mean. In fact, means should never be reported without accompanying standard deviations.

Here is one way to remember what the standard deviation tells you. Suppose you are attending a conference and are offered your choice of two dorm rooms for your housing. The only difference between the two rooms has to do with the plumbing. Because it is farther from the water heater, the shower water temperature in one room fluctuates more than in the other. Let's say that the hot water in Room 652 has a mean temperature of 100 degrees and a standard deviation of 6 degrees. Room 247 also has a mean temperature of 100 degrees but its standard deviation is only 2 degrees. Assuming that the distribution of water temperatures resembles a bell-shaped curve (much more about this in the weeks ahead), the person showering in Room 247 will generally experience hot water temperatures between 96 and 104 degrees 95% of the time - generally tolerable. Consider the person showering in Room 652. The hot water temperature in that shower will fluctuate between 88 and 112 degrees 95% of the time. [The range of temperatures reflects plus or minus two standard deviations from the mean of 100 degrees.] Which room would you pick?

How does this apply to educational settings? Would you prefer to teach in a classroom where the standard deviation of students' reading scores is large or small? Of course, this is not a math question. Students with different skill levels can benefit from interaction with more and less capable peers. Large fluctuations in prerequisite skill levels can serve to frustrate the teacher as well as the students, however. If you are an administrator and you don't really understand standard deviations, you might create classrooms where the mean score levels of students are equal but where some classrooms have more variation than others. As we are focusing on raising mean scores of students, leaving no students behind, should we set goals to increase standard deviations as well or should these be decreasing?