Statistical
Inference, Sampling, and Probability
Descriptive and Inferential
Statistics
The study and use of statistics is roughly divided
into two categories: descriptive statistics and inferential statistics.
As previous sections have demonstrated, descriptive statistics
summarize, organize, and illustrate distributions of numerical
observations. Among typically employed descriptive statistics are
measures of central tendency (e.g., mean, median, mode), measures of
dispersion (e.g., range, interquartile range, variance, standard
deviation), and bivariate measures (e.g., correlation coefficients).
Within the category of descriptive statistics are the visual displays
of distributions, including frequency tables, histograms, pie charts,
bar charts, and scatterplots.
So what is different
about inferential statistics? Instead of simply attempting to summarize
and organize a distribution of data, inferential statistics are used to
extend results generated from a subgroup of observations to a larger
context - in other words, the purpose
of inferential statistics is to generalize from samples to
populations. This section will describe the fundamental
concepts of the process of using inferential statistics.
A
research hypothesis is the focal point of statistical inference. A
research hypothesis makes a prediction, based on a theoretical
foundation, that identifies an anticipated outcome - for example,
higher reading scores, due to a new instructional technique. The
research hypothesis is generated from a, usually broader, research
question. An example of a research question might ask whether there is
a difference between a new way of teaching and a traditional method.
Research questions, in turn, are narrower investigations of a more
general research purpose, which seeks to address an important
problem in the field. So,
you can think of a research hypothesis as the end of a series of
narrower, more focused, statements about a research topic.
A research
hypothesis aids the research study by providing a very specific and precise prediction to
test. The test of the hypothesis involves sampling and then collecting
data. The nature of the sample affects the ability of the researcher to
generalize the results. A full introduction to sampling techniques is
beyond the scope of this introduction, but the important aspect of
sampling for statistical purposes involves the concept of
representation. A quantitative researcher intends to apply her results
to a larger group than the one she studied. The larger group is called
the population. In order
to generalize, the group involved in the study, called the
sample, must resemble the population on variables that are important to
the research. The simplest, but usually costliest, way to
sample is randomly - the equivalent of pulling names out of a hat. This
process is usually costly in terms of time, money, and logistics; so, a
compromise is made for practical reasons. The compromise, and the act
of sampling itself, introduce errors in the process; in other words,
the smaller sample may differ from the population in some important
way. A researcher cannot know whether this situation has actually
happened though. Instead, the researcher will use statistics to
describe the sample's characteristics and then infer from those sample
characteristics what the properties of the larger population are. For
example, testing a new reading method on a properly selected subset of
all third-grade students allows a researcher to make statements about
the value of the reading program for all third-grade students. Numbers pertaining to the sample are
called statistics, and numbers
pertaining to the population are called parameters.
Statisticians use different symbols to distinguish the two set of
numbers. Latin symbols
(e.g., X,
s,
r) are used to represent sample statistics, and Greek symbols (e.g., μ,
σ, ρ) [named mu, sigma, and rho] are used to represent population
parameters. Here are several relationships to remember:
- Symbols
for the mean: X
(sample mean)
is used to estimate μ (population
mean)
- Symbols for the standard
deviation: s (sample
standard deviation) is used to estimate σ (population standard deviation)
- Symbols
for the Pearson correlation coefficient: r (sample correlation)
is used to estimate ρ (population
correlation)
As a researcher who is
interested in improving the state of the field, you might propose to
start your investigation by assuming your research hypothesis is indeed
correct and looking for evidence to the contrary. This approach might
result in a less than objective view of the research study. Instead
researchers start with what is called a null
hypothesis, which
represents the status quo, for example, that there are no
differences between a new method and a traditional one. The null hypothesis makes a statement
about the population that is not directly testable. The
statement is untestable in practice due to time, money, and logistical
constraints, not untestable theoretically. If it was logistically
possible, the new method could be tested on the entire population and
the need to make an inference would not exist.
Here
are some examples of null hypotheses:
Comparison of
treatment (t) and control (c) group means
H0: μt = μc
Comparison
of pre-test (pre) and post-test (post) means
H0: μpre = μpost
Test
of linear relationship between age (a) and experience (e)
H0: ρae = 0
Notice
that null hypotheses assume equality among groups, between variables,
or over time. Researchers then collect data to see if there is evidence
to the contrary. In this way, the null hypothesis provides a benchmark
for assessing whether observed differences are due to chance or some
other factor/variable (i.e., systematic differences).
Here
are a few examples of research hypotheses, also called alternative
hypotheses. These are directly testable because they refer to the
sample statistics using Latin symbols, and not the population
parameters. Notice that these research hypotheses contradict the
equality represented by the null hypotheses. Research hypotheses can
be directional
(i.e., predicting that one statistic is greater than or less than the
other) or they can be non-directional
(i.e., predicting that the two statistics are different but not
specifying how they differ).
Directional
hypothesis that treatment (t) group mean is greater than control (c)
group mean
H1: Xt
> Xc
Non-directional
hypothesis that pre-test (pre) and post-test (post) means are different
(i.e., not equal)
H1: Xpre ≠ Xpost
Directional
hypothesis that a direct (i.e., positive) linear relationship between
age (a) and experience (e) exists
H1: rae > 0
Well
written hypotheses should have the following characteristics. They
should:
- Be declarative statements making
specific predictions.
- Identify a specific expected
relationship.
- Have a firm theory
or literature base.
- Be concise and to the
point.
- Be testable - allowing for the collection of
data measuring variables in a systematic, unambiguously way.
Probability and the Normal
Curve
Probability is the mathematical study of chance. Early
applications of probability involved understanding games of chance,
which can be viewed as repetitions of independent events. For example,
if you flip a coin multiple times, each coin flip is independent of the
previous one and next one. Similarly, if you roll a pair of dice
repeatedly, each roll is independent of the previous one or next one.
The chance that you will see heads on a single coin flip is always the
same - .5 or 1 out of 2, because there are two possible outcomes and
heads is one of those. If you flip a coin 10 times, however, you
probably won't see exactly five heads - there may be six or four or
even nine heads. It is possible, although unlikely with a fair coin, to
see all 10 flips result in heads.
Consider another
example to understand about probability. Suppose you are rolling a pair
of dice repeatedly and adding up the dots on the top of each die. A die
has six sides, numbered 1 to 6. Because you are adding two dice, the
possible sums range between 2 (for snake-eyes - two 1s) and 12 (for
box-cars - two 6s). Here is a table of the possible combinations of
dice. The number appearing on the dice are indicated by the row and
column labels and the sums are shown in each interior cell.
Values
for Dice |
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 6 |
7 |
8 |
9 |
10 |
11 |
12 |
There
are 36 (6x6) possible outcomes, some of which result in the same sum.
For example, a sum of 7 can occur six different ways. Notice that there
is only one way to obtain a sum of 2 and one way for a 12. These are
the least likely sums. The probability associated with each sum is the
ratio of the number of ways it can occur divided by the total number of
possibilities. For example, the probability of obtaining a sum of 3 is
2 out of 36 or .056 presenting 5.6% of the potential outcomes. What is
the probability of obtaining a sum of 11, or 8, or 5? What sum is the
most likely?
If you repeatedly rolled two dice
many, many times and record the sums that you obtained, their
frequencies would eventually resemble the pattern shown in the table.
By counting the number of times 7 occurred, for example, and dividing
that number by the number of rolls, you can calculate the relative frequency of a sum
of 7. Over many repetitions of the dice roll, the relative frequencies get closer and closer
to the theoretical
probabilities. This is called the Law
of Large Numbers.
Graphing
the probabilities results in the following pattern. Instead of two
dice, if you rolled three the pattern would begin to look more
bell-shaped. The more dice involved, the closer the pattern gets to the
normal (bell-shaped) curve. This is called the Central Limit Theorem.
Relating this back to our context of sampling and making inferences,
when drawing a random sample from a population and
calculating the mean for a variable many times independently, the shape
of the resulting distribution of means will be resemble the normal
curve.
Reading
about sampling and the Central Limit Theorem and viewing pictures
doesn't convey the message as well as seeing the process unfold through
an animation. Visit this site (http://www.ruf.rice.edu/~lane/stat_sim/sampling_dist/index.html),
read the instructions, and experiment with drawing different sized
samples from different types of population distributions.
Properties
of Normal
Distributions

There
are actually infinitely many normal distributions - they differ by the
value of their means and standard deviations. Here are some important
properties of normal distributions:
- The
distribution is symmetric, which results in the mean, median,
and mode all being equal.
- The area
under the plot of the distribution (i.e., area between the x-axis and
the curve) equals 1, representing 100% when considered as relative
frequencies.
- The height of the curve approximates a
relative
frequency, but the area under any single point is 0.
- The
tails
(left and right extremes) of the curve approach, not never touch, the
x-axis (i.e., the tails are asymptotic to the x-axis).
Use
of the Normal Distribution
Any raw score from a normal distribution can be mapped onto a
normal curve if the mean and standard
deviation associated with the raw score is known. The graph below
illustrates the mapping of several different types of scores. Notice
that percentiles can be derived from the curve as well.
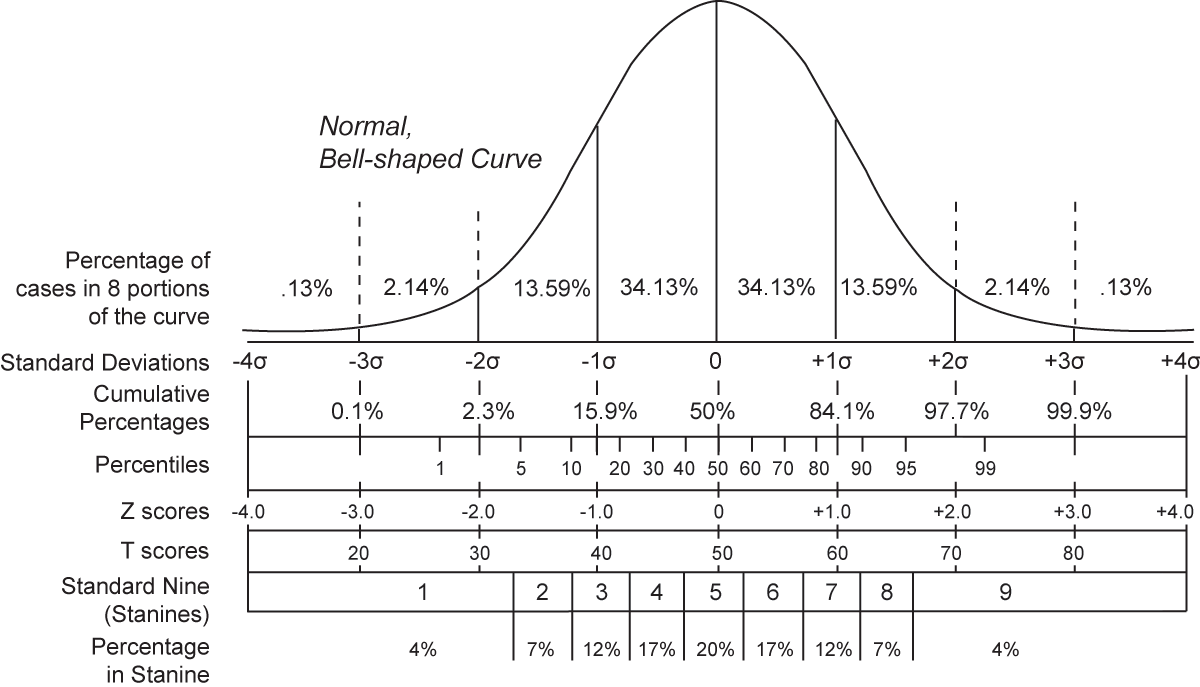
Notice
that approximately 68% of the cases are within one standard deviation
of the mean, 95% are within two standard deviations, and over 99% are
within three standard deviations.
The
Standard Normal Distribution
Even though there are many
normal distributions, one of those has been designated to be the
"standard" normal distribution. The
standard normal distribution is the
normal distribution with a mean of 0 and a standard deviation of 1.
Notice the line labeled Z scores in the graph above. Compare this line
to the line labeled Standard Deviations just below the x-axis. Notice
that a z
score of +1.0 corresponds to a point under the curve labeled +1σ.
Any raw score can be converted to a z
score and back using these formulas:
z = (X - X) / s
and
X = s * z + X
where X is the mean of
the distribution of raw scores and s is the standard deviation of the
distribution of raw scores.
Here is an example of how to use the conversion formulas:
Suppose you have a score of 15 on a test where the mean was 10 and the
standard deviation was 2.5. The z
score equivalent to a raw score of 15 is
z = (15 - 10) / 2.5 = 5 / 2.5
= 2
Another
way to describe this score is that it is 2 standard deviations above
the mean. In a normal distribution, a score of raw score of 15 would be
higher than 97.7% of the other scores. Look at the graph above to
locate the source of 97.7%.
Here is a related example. Suppose
you wanted to provide extra help to anyone who scored more than one
standard deviation below the mean. What raw scores should you look for?
Scoring one standard deviation below the mean results in a z score of -1. To determine the
associated raw score, use the second conversion formula
X = 2.5 * (-1) + 10 = -2.5 + 10 = 7.5
Anyone
scoring 7.5 or lower would be offered extra help. By inspecting the
graph above, can you determine what percentage of scores this would
represent?
Converting to z scores
allows raw scores from different testing situations to be compared. For
example, which is better a 20 in Ms. Chan's class where the mean was 12
and the standard deviation was 6, or a 15 in Mr. Williams' class where
the mean was also 12 but the standard deviation was 2? Let's compare
the z scores.
zc = (20 - 12) / 6
= 8 / 6 = 1.3
zw = (15 - 12) / 2
= 3 / 2 = 1.5
The 15 in Mr. Williams' class is better than the 20 in Ms. Chan's
class, by .2 standard deviations.
Visit this site (http://psych.colorado.edu/~mcclella/java/normal/normz.html)
to use an applet that will convert a raw score, with its associated
mean and standard deviation, to a z
score. This site (http://davidmlane.com/hyperstat/z_table.html)
calculates the area under the curve for different z values and
intervals.





